Matemática sob medida
Saiba como ensinar cálculos e proporções de forma simples e lúdica

Uma das primeiras impressões sobre tamanhos e medidas que os alunos têm na escola está diretamente ligada à fila. Do maior ao menor os pequenos estudantes são enfileirados para se locomoverem pela instituição de ensino. Essa prática simples que se apresenta diariamente pode ser utilizada para ensinar cálculos e proporções. A Revista Appai Educar conversou com o professor de matemática Fabiano Almeida, que leciona nas redes municipais de São João de Meriti, Belford Roxo e Japeri. Nessa matéria exclusiva, ele sugeriu ideias de ouro para ensinar as crianças da segunda a quinta série.
É na Educação Infantil que os pequenos estudantes aprendem que medir significa comparar grandezas. Quando esse conteúdo é trabalhado de forma eficaz, o rendimento no Ensino Fundamental I melhora muito, afinal a medição está diretamente ligada não só à geometria e à estatística, mas também a outras disciplinas. Por exemplo, nas ciências da natureza, medir é essencial. Nas humanas, usa-se escalas e, especialmente, marcações de tempo. E nas artes há as noções de proporcionalidade. Ao explorar esse conceito além dos muros da escola, os alunos podem praticar o raciocínio com os afazeres dentro de casa, como uma receita culinária, uma medicação e até analisar a estrutura de sua moradia.
De acordo com o professor Fabiano, ao indicar esse tipo de atividade, as crianças rapidamente descobrem que a padronização foi criada para facilitar a vida. “E isso é fácil de fazer com instrumentos como fita métrica, trena e régua. Descrevo as partes, a função e conto um pouco da história. Quase todos já viram alguém usando”, explica o docente acrescentando que a fita é a que chama mais atenção nessa iniciação sobre o conhecimento das medidas. “Nesse primeiro momento me concentro em ensinar as unidades usadas pela região urbana e não as gerais. Então firmo atividades sobre metros e quilômetros, deixando para um outro momento hectares, por exemplo, apesar de sempre surgir a curiosidade, principalmente daqueles alunos que vivem em áreas rurais”, ratifica.
Quanto mais grandezas forem comparadas, mais enxuto será o repertório adquirido. Fabiano também trabalha com unidades de tempo, para diversificar a atividade. O conjunto dia, mês e ano é instigado partindo de uma premissa bastante simples: quantos meses faltam para as férias? Nesse primeiro momento, o professor disse que ninguém sabe responder. Para que eles entendam o conceito, apenas explicar expondo calendário basta. Quando todos ficam craques em consultar as datas, Fabiano propõe um desafio: o de fazer o próprio calendário.

Aprendendo com os gráficos
Basta abrirmos um jornal, uma revista ou assistirmos a televisão para percebermos que, cada vez mais, a estatística é incluída no nosso cotidiano e no de nossos estudantes. Informações de toda natureza passam rapidamente sob nossos olhos em forma de gráficos e tabelas. Este se tornou um hábito muito comum no dia a dia de qualquer pessoa, mas será que os livros didáticos estão vendo essas formas de expor conteúdo como uma linguagem usual a ser ensinada?
Apresentar estatística para as crianças desde o período de alfabetização tornou-se uma necessidade social. Não pensamos o seu ensino como um amontoado de fórmulas e cálculos, mas em desenvolver no aluno a habilidade de coletar, organizar, interpretar e tomar decisões frente aos dados, utilizando como ferramenta a estatística.
Esta, por sua vez, passou a ser alvo de muitos educadores e livros didáticos a partir dos Parâmetros Curriculares Nacionais (PCN) do Ensino Fundamental, em 1997. Mas até hoje com a Base Nacional Comum Curricular (BNCC) ela ainda é norteadora por sua importância nas diferentes formas de representar as informações matemáticas e a sua relação significativa com a realidade do aluno.
O professor Fabiano Pereira relata a atividade da seguinte forma: “Se você estiver com um grupo de crianças pergunte para elas quem é a mais alta da turma. Aí vem a parte prática! Pegue um pedaço de barbante e corte medindo esse aluno, e em seguida todos vão marcar um outro pedaço com a sua própria altura. Compare os tamanhos dos dois e pergunte de quem é cada um deles. No próximo passo pegue uma fita métrica ou uma trena e meça cada pedaço de barbante, anote em um papel o nome da pessoa medida com aquele barbante e, ao lado, sua altura.
Em um segundo momento trabalhe com o peso. Para isso você vai precisar de uma balança. Se não tiver uma na escola faça um passeio com os alunos e leve-os até uma farmácia ou lugar que possua. Não se esqueça de anotar o peso de cada um também ao lado do nome correspondente. Compare os pesos, explique que 1.000 miligramas = 1 grama; que 1.000 gramas = 1 quilograma; e que 1.000 quilogramas = 1 tonelada. Seja lúdico ao falar sobre miligramas e toneladas, medidas mais distantes da realidade da criança. Explique que apenas algo muito leve, como uma formiga, pesa miligramas e que coisas bem pesadas, como elefantes, chegam a toneladas. Depois dessa explicação e da tabela mostrando a altura e o peso da criança façam juntos comparações”, diz o docente.
Para estimular que os pequenos se questionem sobre seu peso e altura pergunte se se acham grandes ou pequenos; ou, caso pudessem se medir com laranjas, quantas frutas acham que precisaria para corresponder à sua altura; ou ainda, pergunte também quantas laranjas seriam necessárias para corresponder ao seu peso.
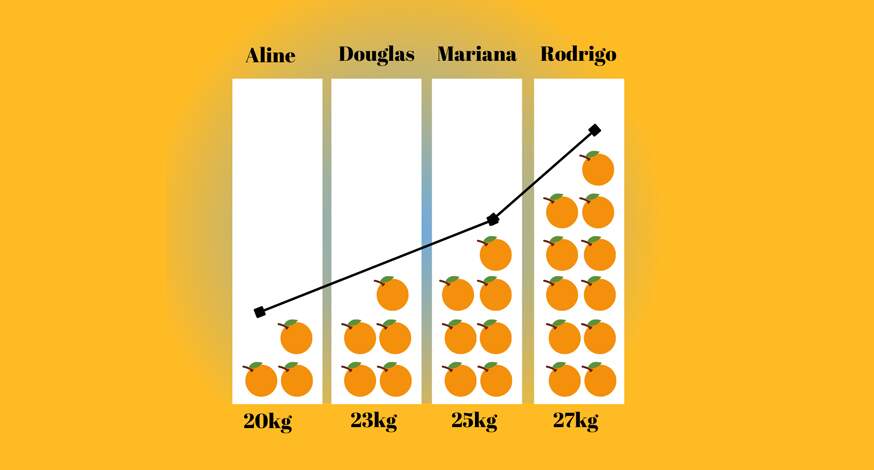
Agora chegou a hora de produzir o gráfico. Peça aos alunos que organizem todas as informações recolhidas e que desenhem num papel retângulos verticais iguais. A quantidade será definida pelo número de alunos. Em cima do retângulo coloque o nome do estudante em ordem alfabética, embaixo o peso referente. Dentro do retângulo desenhe a quantidade de laranjas que representa o peso de cada aluno. Ao fim, faça uma linha entre o ápice das laranjas para ver a diferença. Veja o exemplo abaixo:
Outras ideias para trabalhar medidas

• O salto mais longo
Para trabalhar unidades como metro e centímetro, organize uma competição de salto em distância. Cada criança realiza três tentativas. Com barbante, um colega mede o resultado de cada uma. Depois, num quadro individual, o autor do pulo coloca os pedaços lado a lado e confere a medida com a fita métrica. Os valores são registrados em papel e comparados. No fim da atividade, as medidas devem estar em ordem decrescente para se descobrir qual foi o salto mais longo.
O salto mais longo: ideia original de Thiago Minami, colaborador da Nova Escola.
• Qual o tamanho do seu pé?
Por meio de uma roda de ideias apresente o poema abaixo e leia com os alunos.

Procure estimular a participação de todos na discussão do poema, propondo as seguintes questões: o pé do gigante é grande ou pequeno?; o seu pé é maior ou menor que o do gigante?; quantos passos o gigante deu para ir de sua casa até o lago?; você daria mais ou menos passos que o gigante para fazer o mesmo percurso? Por quê?
Proponha aos alunos que descubram a distância da porta da sala de aula até a mesa da professora. Em um primeiro momento eles escrevem no papel (em seu caderno de Matemática) qual a distância que acreditam que possui esse espaço. Depois, cada um deverá utilizar os seus passos para fazer a sua medição sem contar para o colega, apenas realizando seu registro. Quando todos terminarem faça uma roda de conversa e exponha os resultados.
É importante que os alunos percebam que, quanto menor o tamanho das pernas e dos pés, maior será a quantidade de passos necessários para traçar o mesmo percurso.
Além da atividade acima, você pode trabalhar com os pequenos questões simples do cotidiano da sala de aula, tais como: “Qual é a mochila maior?”; “Quem é o aluno mais alto?”; “Quem é o aluno mais baixo?”; “Qual a distância da lixeira até a porta da sala de aula”?; “Qual a altura do armário da sala de aula?”.
Em seguida, como registro no caderno de Matemática, proponha algumas medições, utilizando partes do seu corpo ou objetos como palitos de picolé.
Qual o tamanho do seu pé? Ideia original de: Juliana Sosso, autora do livro Coleção Agora é Hora. Alfabetização Matemática. 1 º Ano. 1. Curitiba: Base Editorial, 2011. p.143.
Por Richard Günter
Fontes: MEC | BNCC | Portal do Professor | Nova Escola































